Innhold

Denne anvisningen gir råd om prosjektering og utførelse av forankring og bevegelsesfuger for murt forblending og skallmurvegger med vanger i mur.

Lastpåkjenning, forventede bevegelser og kapasiteten til trådbinderne danner grunnlag for dimensjonering av forankringsløsninger. Anvisningen viser også anbefalt utførelse for vanlige forankringsløsninger som både ivaretar konstruksjonssikkerhet og byggetekniske krav.

Dimensjoneringsprinsippene gjelder for runde, rette trådbindere av rustfritt stål, men er også aktuelle for andre typer tråd- og metallbindere.

×

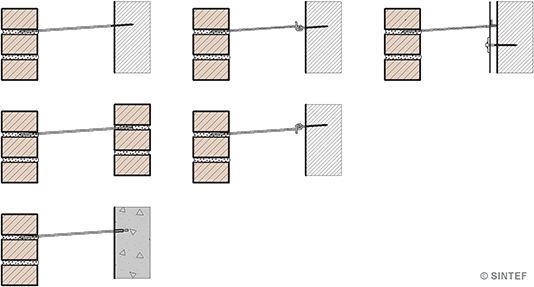
Forankringens funksjon er å overføre horisontallaster som trykk og strekk i trådbindernes lengderetning. Samtidig må forankringen tåle sideveis forskyvning i veggplanet som følge av fukt- og temperaturbevegelser.

Lukk

1Definisjoner og krav

11Murt forblending

Murt forblending er en fasadekledning i mur som er forankret til den bakenforliggende veggen, men forblendingen bidrar ikke til konstruksjonens stabilitet og bæreevne.

Forblendingen forankres til bygningens hovedbæresystem med trådbindere.

Se Byggdetaljer 542.301 for prinsipp og oppbygging av murt forblending.

12Skallmurvegg

Skallmur er en bærende yttervegg som består av to murte vanger (veggdeler) med et isolert og drenert hulrom. Skallmuren fungerer som bæresystem, fasadekledning og innvendig overflate.

Ytre og indre vange i skallmuren forankres effektivt sammen med trådbindere for å oppnå samvirke.

Se Byggdetaljer 523.231 for prinsipp og oppbygging av skallmurvegger.

13Bevegelsesfuge

Murverk endrer volum ved variasjoner i fuktinnhold og temperatur.

Ved prosjektering må man ta hensyn til bevegelser i veggplanet. For store veggfelter kan bevegelser føre til skader på forankringen, selve veggfeltet og tilstøtende konstruksjoner. For å motvirke skader bør fasader deles opp i mindre veggfelter med bevegelsesfuger. Se pkt. 2.

14Forankring

Forankringen skal ta opp og overføre laster til bygningens hovedbæresystem. Samtidig må forankringen tåle sideveis forskyvning i veggplanet som følge av fukt- og temperaturbevegelser. I skallmurvegger skal forankringen i tillegg sikre samvirke mellom murvangene.

15Korrosjonsbeskyttelse

Trådbinderne må ha tilstrekkelig korrosjonsbeskyttelse til å kunne stå i bygningens levetid. Til forankring brukes trådbindere av rustfritt stål for eksponeringsklasse MX1 til og med MX4; for MX5 (kjemisk eksponering) benyttes syrefaste bindere i henhold til NS-EN 1996-1-1.

16Forankringssystem

Det fins i hovedsak tre ulike forankringssystemer, avhengig av hvordan trådbinderne festes til bakveggen. Se tabell 16. Hvilket forankringssystem man skal bruke, avhenger av hvilke påkjenninger man kan forvente på trådbinderen. Se pkt. 5 om belastninger.

Tabell 16

Oversikt over de tre vanligste forankringssystemene med tilhørende egenskaper

Deformasjonsegenskaper	Type forankringssystem
	Faste trådbindere	Leddede trådbindere	Forskyvelige trådbindere
	× Lukk	× Lukk	× Lukk
	Faste trådbindere har stor trykkapasitet, men liten evne til å tåle sideveis forskyvning.	Leddede trådbindere er leddet i én ende. De har middels trykkapasitet og middels evne til å tåle sideveis forskyvning.	Trådbindere med forskyvelig ende har liten trykkapasitet, men tåler ubegrenset forskyvning i skinnens lengderetning.
Deformasjon av trådbinder ved sideveis forskyvning	× Lukk	× Lukk	× Lukk
Deformasjon av trådbinder ved trykkbelastning	× Lukk	× Lukk	× Lukk

17Ytterste trådbinder

Trådbinderen som er plassert lengst fra nullpunktet for bevegelse, vil være mest utsatt for bevegelse fra temperatur- og fuktutvidelse og omtales i anvisningen som ytterste trådbinder. Nullpunktet for bevegelse er beskrevet i pkt. 22. Figur 17 viser plasseringen av ytterste trådbinder på et veggfelt og hvilke krefter den utsettes for.

×

Fig. 17

Ytterste trådbinder er den trådbinderen i et veggfelt som er plassert lengst fra nullpunktet for bevegelse. Ytterste trådbinder vil ofte være bestemmende for hvilket forankringssystem man kan bruke. Den må tåle påkjenninger som følge av temperatur- og fuktbevegelser samtidig som den skal ta opp andre påførte laster som horisontallast.

Lukk

18Fri binderlengde

Avstanden mellom yttervangen og bakveggen – fri binderlengde – er avgjørende for trådbinderens kapasitet. Stor fri binderlengde gjør at trådbinderen tåler tverrforskyvning godt, men er utsatt for knekking. Ved liten fri binderlengde tåler trådbinderen tverrforskyvning dårligere, men er mindre utsatt for knekking.

For en skallmurvegg vil fri binderlengde være avstanden mellom innvendig side av ytre og indre vange.

For en forblending med skrubindere er fri binderlengde avstanden mellom innvendig side av murvangen og trevirket. Hvis skrubinderen festes i en bakvegg med vindsperreplater, ser man bort fra platetykkelsen ved bestemmelse av fri binderlengde, se fig. 18.

For en forblending med slagbindere er fri binderlengde avstanden mellom innvendig side av murvangen og betongen den festes i, se fig. 18.

×

Fig. 18

Prinsippskisse for fri binderlengde

1. Skrubinder

2. Slagbinder

Lukk

19Krav til dokumentasjon av produktegenskaper

191Generelt

For å kunne bygge produkter inn i byggverk skal prosjekterende spesifisere hvilke egenskaper som er nødvendige for at det ferdige byggverket tilfredsstiller kravene i byggteknisk forskrift. De ansvarlige i byggesaken skal påse at produktene er egnet og at det er dokumentert at produktene har de egenskapene som er spesifisert.

Se Byggdetaljer 570.001 for mer informasjon om produktdokumentasjon og CE-merking.

For produkter som markedsføres og selges i Norge, skal det foreligge en ytelseserklæring (Declaration of Performance, DoP) på norsk, svensk eller dansk.

192CE-merking av bindere

Veggbindere, herunder trådbindere, skal CE-merkes i henhold til harmonisert produktstandard NS-EN 845-1. Kapasitetene testes etter standarden NS-EN 846-5 (tosidig prøving) eller NS-EN 846-6 (ensidig prøving). Ved prøvingen benyttes innmuringsdybde, helning og bevegelse som deklarert av produsent. Dette er spesielt viktig for andre typer bindere enn rette trådbindere av stål, der kapasitet ikke kan beregnes ut fra kjent teori. Leverandører som er definert som mikrobedrifter, er fritatt fra kravet om prøving av utpekt kontrollorgan og kan selv prøve egne veggbindere.

Man bør kontrollere at ytelseserklæringen inneholder dokumentasjon om relevante egenskaper og at ytelsene er tilstrekkelig for det aktuelle formålet.

2Oppdeling i veggfelter med bevegelsesfuger

21Generelt

For å unngå skader fra bevegelser som følge av temperatur- og fuktutvidelse deles større fasader opp i mindre veggfelter med bevegelsesfuger. Veggfeltene bør mures på glidesjikt, og man kan benytte fugearmering.

Veggfeltene skal være atskilt fra andre konstruktive elementer slik at de har mulighet for fri bevegelse. Mulighet for fri bevegelse er spesielt viktig ved forankring til stive konstruktive elementer som stål og betong. Sammentrekning ved temperaturfall eller tørking gjør at selv en liten fastholding kan føre til oppsprekking fordi murverket har liten strekkapasitet.

Veggfelter over horisontale bevegelsesfuger har oftest separat bæring, se pkt. 256, og man kan benytte horisontale bevegelsesfuger under utkraget murverk.

22Nullpunkt for bevegelse og avstand til ytterste binder

Nullpunktet for bevegelse er det punktet på et veggfelt som man antar forholder seg i ro selv om veggfeltet utvider seg eller trekker seg sammen. Nullpunktet for bevegelse må velges før man kan dimensjonere forankringssystemet.

For et veggfelt som ikke ligger på et glidesjikt, kan man velge nullpunkt for bevegelse på samme måte som for veggfelt på glidesjikt.

Når nullpunkt for bevegelse er fastsatt, kan man beregne avstanden, r, ut til ytterste binder. Se fig. 22. Avstand, r, til ytterste binder er avgjørende for å velge forankringssystem.

×

Fig. 22

Oppriss av fasade

Eksempel på fastsetting av nullpunkt for bevegelse og plassering av bevegelsesfuger. Stiplet gul linje, r, viser avstand fra nullpunkt for bevegelse til ytterste binder. Ommurte hjørner plasserer nullpunkt for bevegelse ytterst på veggfeltet. For veggfelter med bevegelsesfuger på begge sider vil nullpunkt for bevegelse plasseres nederst i midten.

Lukk

Korte utkraginger i form av horisontale bevegelsesfuger inntil ca. 0,5 m, kan normalt utføres uten ny bæring, med armering i horisontalfugene.

23Avstander til ytterste trådbinder

Tabell 23 a–c angir veiledende maks avstand, r, fra nullpunkt for bevegelse til ytterste trådbinder som beskrevet i pkt. 22.

Bruk av tabellene gjøres ut fra følgende kjente data:

• avstand fra nullpunkt for bevegelse til ytterste binder, se pkt. 22

• fri binderlengde, se pkt. 18

• diameter på trådbinder

• stålkvalitet på trådbinder

Se pkt. 54 for detaljer om forutsetninger og beregninger.

Tabell 23 a

Avstand til ytterste binder for faste trådbindere. Veiledende dimensjoner. Forutsetninger for verdiene er gitt i pkt. 5.

Faste trådbindere	Største avstand fra nullpunkt for bevegelse, r1)
× Lukk	Stål med karakteristisk flytegrense, fyk = 500 N/mm2		Stål med karakteristisk flytegrense, fyk = 700 N/mm2
Fri binderlengde (mm)	Diameter 4 mm	Diameter 5 mm	Diameter 4 mm	Diameter 5 mm
50	3,8 m	3,2 m	5,3 m	4,5 m
75	7,7 m	6,5 m	11 m	9,1 m
100	13 m	11 m	18 m	15 m
125	20 m	16 m	28 m	23 m
200	49 m	40 m	68 m	56 m

1. Største forskyvning ut fra nullpunkt for bevegelse er antatt å være ±0,25 mm/m, som for tegl, se pkt. 52.

Tabell 23 b

Avstand til ytterste binder for leddede trådbindere. Veiledende dimensjoner. Forutsetninger for verdiene er gitt i pkt. 5.

Leddede trådbindere	Største avstand fra nullpunkt for bevegelse, r1)
× Lukk	Stål med karakteristisk flytegrense, fyk = 500 N/mm2		Stål med karakteristisk flytegrense, fyk = 700 N/mm2
Fri binderlengde (mm)	Diameter 4 mm	Diameter 5 mm	Diameter 4 mm	Diameter 5 mm
50	7,6 m	6,5 m	11 m	9,1 m
75	15 m	13 m	22 m	18 m
100	26 m	22 m	37 m	30 m
125	40 m	33 m	56 m	46 m
200	97 m	79 m	136 m	111 m

1. Største forskyvning ut fra nullpunkt for bevegelse er antatt å være ±0,25 mm/m, som for tegl, se pkt. 52.

Tabell 23 c

Avstand til ytterste binder for forskyvelige trådbindere. Veiledende dimensjoner. Forutsetninger for verdiene er gitt i pkt. 5.

Forskyvelige trådbindere	Største avstand fra nullpunkt for bevegelse, r
× Lukk	Stål med karakteristisk flytegrense, fyk = 500 N/mm2		Stål med karakteristisk flytegrense, fyk = 700 N/mm2
Fri binderlengde (mm)	Diameter 4 mm	Diameter 5 mm	Diameter 4 mm	Diameter 5 mm
	Skinnesystemer med forskyvelige trådbindere kan ha ubegrenset avstand fra nullpunkt for bevegelse til ytterste trådbinder i skinnas lengderetning.   Største avstand fra nullpunkt for bevegelse på tvers av skinnas lengderetning er som for leddede trådbindere, se tabell 23 b. Det vil si at ved vertikal montering av skinner blir maks horisontal avstand fra nullpunkt for bevegelse til skinne tilsvarende «r» i tabell 23 b.   Se eksempel på bruk av tabell i pkt. 64.

24Avstand mellom vertikale bevegelsesfuger

241Største anbefalte horisontale avstand mellom bevegelsesfuger

Største anbefalte horisontale avstand mellom vertikale bevegelsesfuger er gitt i tabell 241. Tabellen er mer detaljert enn anbefalingene gitt i NS-EN 1996-2.

242Materialegenskaper påvirker veggfeltets bevegelser

Fargen på steinen har betydning for hvor mye varme den absorberer, noe som videre kan ha betydning for hvor stor temperaturutvidelsen kan bli.

Forholdet mellom fastheten til steinen og mørtelen har betydning for hvordan sprekkdannelser oppstår. Svakere mørtel vil gi mange små sprekker i fugene, mens en svakere stein kan føre til sprekker tvers gjennom både stein og fuger. Årsaken til man kan se lange fasader på historiske bygninger uten bevegelsesfuger og uten synlige sprekker, er kombinasjonen av svak mørtel og sterk stein.

25Plassering av bevegelsesfuger

251Hjørner

I en vegg med murt forblending er det en enkel løsning å plassere bevegelsesfuger i hjørner, se fig. 251. Ommurte hjørner kan være ønskelig av stabilitetshensyn, spesielt for skallmurvegger, men de kan også velges av estetiske hensyn.

×

Fig. 251

Eksempler på hjørner

1. Hjørne med bevegelsesfuge

2. Ommurt hjørne uten bevegelsesfuge

Lukk

252Minste vegglengde

I henhold til NS-EN 1996-1-1 skal en murvegg ha et minste tverrsnittsareal på 0,04 m². For en vange med tykkelse på 100 mm blir dermed minste tillatte vegglengde 400 mm, se fig. 252.

For alle murvegger med mindre tverrsnittsareal enn 0,1 m² skal trykkfastheten reduseres i henhold til NS-EN 1996-1-1.

×

Fig. 252

Minste tillatte netto vegglengde, a, er 400 mm for en 100 mm tykk vange.

Lukk

253Sprang i opplegg for veggen

En vegg med opplegg på flere nivåer gir lett låsing av murveggen, og bevegelsesfuger bør plasseres ved sprangene, se fig. 253.

I en vegg med opplegg på flere nivåer anbefales det mindre avstand mellom bevegelsesfugene. Avstanden bør ikke være større enn det halve av avstandene gitt i tabell 241 (uten glidesjikt). Det bør også plasseres bevegelsesfuger slik at største høydeforskjell på fundamentet til et sammengende veggfelt ikke overskrider én etasjehøyde.

×

Fig. 253

Eksempel på bevegelsesfuge som er plassert ved et sprang i opplegget til veggen. Bevegelsesfugen er plassert i det spranget som gjør at vegglengden mellom bevegelsesfuge og vindusåpning blir så stor som mulig.

Lukk

254Ulike høyder

Der veggen har opplegg på ett nivå, men hvor vegghøyden er vesentlig forskjellig, anbefaler vi å plassere bevegelsesfuger i skillet mellom høy og lav vegg, se fig. 254.

×

Fig. 254

Oppriss av fasade

Også der veggen har opplegg på samme nivå, anbefales det å plassere en bevegelsesfuge i overgangen mellom høy og lav vegg.

Lukk

255Sprang i veggliv

Der det er et sprang i veggen slik at veggplanet flyttes inn eller ut via to hjørner, bør man skille veggplanene med en bevegelsesfuge i innvendig hjørne, se fig. 255 (I). Der man ønsker doble ommurte hjørner uten bevegelsesfuge, bør avstanden mellom planene være minst én meter, se fig. 255 (II). Avstanden fra spranget til neste bevegelsesfuge bør ikke være større enn det halve av avstandene gitt i tabell 241. Hjørnene bør armeres for hver halve høydemeter, og det bør mures på glidesjikt. Det benyttes ikke bindere i spranget, som er den delen av veggen som står normalt på resten av veggen.

×

Fig. 255

Eksempler på sprang i fasade. Horisontalsnitt

1. Små sprang under 1 m bør utføres med bevegelsesfuge i innvendig hjørne.

2. Større sprang kan mures gjennomgående dersom avstanden fra hjørne/bevegelsefuge til spranget er under halvparten av avstandene i tabell 241.

Lukk

256Horisontale bevegelsesfuger

For høye bygninger, over 20 meter, vil relative bevegelser mellom en forblending og bakveggen kunne skape problemer. En løsning kan være horisontale bevegelsesfuger som plasseres for eksempel i hver fjerde etasje. Veggfeltet over bevegelsesfugen må ha egen bæring i form av konsoller eller annet, se fig. 256. Dette må man ta hensyn til ved prosjekteringen av bygningens hovedbæresystem.

×

Fig. 256

Eksempel på horisontal bevegelsesfuge i forblendingen. Stålkonsoller gir ny bæring av veggfeltet over bevegelsesfugen. Vertikalsnitt

Lukk

3Antall og plassering av trådbindere

31Generelt

Antall trådbindere beregnes og angis per veggareal. Antall trådbindere må være tilstrekkelig til å oppta lastene veggen utsettes for. Særlig langs kantene er det viktig med tilstrekkelig forankring. Siden vindlast er sterkest langs endene av veggen, bør trådbinderne plasseres så tett på hjørnene og toppen som mulig. Der man har binderfrie soner mot ommurte hjørner eller trådbindere uten beregningsmessig kapasitet, må man kompensere med tettere avstand mellom trådbinderne i resten av veggfeltet.

Der trådbinderne kommer i konflikt med fugearmering eller annet, bør trådbinderne flyttes til første skift de kan monteres i uten å komme i konflikt. Trådbindere øverst i et veggfelt vil ha redusert kapasitet på grunn av begrenset egenlast fra veggfeltet over innfestingspunktet.

32Minste antall trådbindere

321Minste antall trådbindere i henhold til NS-EN 1996-1-1

Antall forankringsfester (trådbindere) skal dimensjoneres på grunnlag av valgt forankringssystem, se pkt. 16. Uavhengig av hvilket forankringssystem man velger, stiller NS-EN 1996-1-1 følgende minstekrav:

• For murte forblendingsvegger kreves minst to trådbindere per kvadratmeter.

• For skallmurvegger kreves minst fire trådbindere per kvadratmeter.

322Minste antall trådbindere for å ta opp opptredende horisontallaster

Antall trådbindere må være tilstrekkelig for å ta opp beregnet horisontallast, og det kan være behov for flere bindere enn minstekravet fra NS-EN 1996-1-1. Trådbinderens kapasitet til å ta opp horisontallast er beskrevet i pkt. 33 og pkt. 34. Når man har fastsatt belastning fra horisontallast og kapasitet per trådbinder, kan antall trådbindere beregnes med følgende formel:

$\displaystyle \frac{\textsf{Belastning per } \mathsf{m^2}}{\textsf{Kapasitet per binder}} < \textsf{Antall bindere per } \mathsf{m^2}$

323Anbefalt antall trådbindere for fastholding av isolasjon

SINTEF anbefaler minst 2,8 trådbindere per kvadratmeter (tilsvarende 0,6 m × 0,6 m) dersom trådbinderne benyttes til fastholding av isolasjon med plastbrikker. For fastholding av isolasjonslag tykkere enn 150 mm anbefales minst fire bindere per kvadratmeter veggflate.

324Anbefalt montasjeforankring

Det kan være behov for flere trådbindere for å sikre stabilitet under muring av for eksempel smale søyler. Slike trådbindere kalles montasjeforankring. I de fleste situasjoner oppnår man god stabilitet under oppmuring ved å benytte 2,8 bindere per kvadratmeter. Smale søyler bør utføres med samme vertikale avstand mellom bindere som resten av veggen.

En vegg kan bestå av trådbindere med og uten beregningsmessig kapasitet. Eksempler på trådbindere uten beregningsmessig kapasitet kan være trådbindere i utfyllende bindingsverk som nevnt i pkt. 36, og trådbindere i toppen av parapet. Slike trådbindere plasseres som regel med samme tetthet som for resten av veggen og fungerer som montasjeforankring ved oppmuring og eventuelt for å holde isolasjon på plass.

33Veiledende trykkapasitet for rette trådbindere av stål

Tabell 33 a–c angir veiledende dimensjoner for trykkapasitet for trådbindere. For eksempel på bruk av tabell 33 a–c, se pkt. 6. Se også pkt. 55 for nærmere beskrivelse av aksialkapasitet for trådbindere.

Bruk av tabell 33 a–c gjøres ut fra følgende kjente data:

• forankringssystem, se pkt. 15

• fri binderlengde, se pkt. 18

• diameter på trådbinder

• stålkvalitet på trådbinder

Tabell 33 a

Dimensjonerende trykkapasitet for faste trådbindere avhengig av fri binderlengde, stålets karakteristiske flytegrense og diameter

Faste trådbindere	Dimensjonerende trykkapasitet1)
× Lukk	Stål med karakteristisk flytegrense, fyk = 500 N/mm2		Stål med karakteristisk flytegrense, fyk = 700 N/mm2
Fri binderlengde (mm)	Diameter 4 mm	Diameter 5 mm	Diameter 4 mm	Diameter 5 mm
50	2 470 N	4 050 N	3 270 N	5 430 N
75	2 140 N	3 660 N	2 690 N	4 760 N
100	1 780 N	3 230 N	2 120 N	4 020 N
125	1 450 N	2 790 N	1 640 N	3 310 N
200	770 N	1 670 N	810 N	1 810 N
250	540 N	1 200 N	560 N	1 270 N
300	390 N	900 N	400 N	930 N

1. Trykkapasiteten er beregnet ut fra knekkapasitet i henhold til NS-EN 1993-1-1. Materialfaktor, $\mathsfit{\gamma}_{\mathsfit{M}}$ = 2,2 i henhold til NS-EN 1996-1-1. Elastisitetsmodul er forutsatt å være E = 200 000 N/mm².

Tabell 33 b

Dimensjonerende trykkapasitet for leddede trådbindere avhengig av fri binderlengde, stålets karakteristiske flytegrense og diameter

Leddede trådbindere	Dimensjonerende trykkapasitet1)
× Lukk	Stål med karakteristisk flytegrense, fyk = 500 N/mm2		Stål med karakteristisk flytegrense, fyk = 700 N/mm2
Fri binderlengde (mm)	Diameter 4 mm	Diameter 5 mm	Diameter 4 mm	Diameter 5 mm
50	2 160 N	3 670 N	2 740 N	4 780 N
75	1 670 N	3 070 N	1 950 N	3 760 N
100	1 230 N	2 460 N	1 360 N	2 830 N
125	920 N	1 930 N	980 N	2 130 N
200	430 N	980 N	450 N	1 030 N
250	290 N	680 N	300 N	700 N
300	210 N	490 N	220 N	510 N
330	180 N	420 N	180 N	430 N

1. Trykkapasiteten er beregnet ut fra knekkapasitet i henhold til NS-EN 1993-1-1. Materialfaktor, $\mathsfit{\gamma}_{\mathsfit{M}}$ = 2,2 i henhold til NS-EN 1996-1-1. Elastisitetsmodul er forutsatt å være E = 200 000 N/mm².

Tabell 33 c

Dimensjonerende trykkapasitet for forskyvelige trådbindere avhengig av fri binderlengde, stålets karakteristiske flytegrense og diameter

Forskyvelige trådbindere1)	Dimensjonerende trykkapasitet2)
× Lukk	Stål med karakteristisk flytegrense, fyk = 500 N/mm2		Stål med karakteristisk flytegrense, fyk = 700 N/mm2
Fri binderlengde (mm)	Diameter 4 mm	Diameter 5 mm	Diameter 4 mm	Diameter 5 mm
50	640 N	1 360 N	670 N	1 450 N
75	340 N	760 N	350 N	790 N
100	210 N	480 N	220 N	490 N
125	140 N	330 N	150 N	340 N
200	60 N	140 N	60 N	140 N
250	40 N	90 N	40 N	100 N
300	30 N	70 N	30 N	70 N
330	20 N	60 N	20 N	60 N

1. Knekkapasiteten påvirkes av binderens friksjon mot skinna i en trykksituasjon. Tabellen tar ikke hensyn til denne effekten. Ta kontakt med leverandør av aktuelt system for dokumentasjon av kapasitet ut over kapasitet angitt her.

2. Trykkapasiteten er beregnet ut fra knekkapasitet i henhold til NS-EN 1993-1-1. Materialfaktor, $\mathsfit{\gamma}_{\mathsfit{M}}$ = 2,2 i henhold til NS-EN 1996-1-1. Elastisitetsmodul er forutsatt å være E = 200 000 N/mm².

34Veiledende uttrekkskapasitet

Tabell 34 viser uttrekkskapasiteter for en trådbinder fra en murvange eller en bakvegg. Tabellen kan benyttes der det ikke er gjort tiltak for å dokumentere høyere uttrekkskapasitet.

35Forankring til betongvegg eller annen stiv heldekkende bakvegg

Er bakveggen i betong eller annet stivt heldekkende materiale, kan den oppta all horisontallast som trådbinderne overfører. Trådbinderne kan da fordeles jevnt og systematisk over veggfeltet.

36Forankring til utfyllende bindingsverksvegg eller annen bakvegg med lav stivhet

Er bakveggen utfyllende bindingsverk eller har en vesentlig lavere eller ukjent stivhet i forhold til yttervangen, må man anta at bakveggen ikke tar opp noe av horisontallasten som trådbinderne overfører. Påførte laster må ledes direkte inn til hovedbæresystemet for bygningen.

Som regel kan man anta at trådbindere som er plassert inntil 4 × stendertykkelse fra svill, overfører krefter via stendere og videre inn i dekkeforkant. Se fig. 36.

×

Fig. 36

Prinsippskisse som viser forankring til utfyllende bindingsverk og betongdekker og -vegger.

Blå kryss representerer trådbindere som kan antas å overføre horisontallaster til bygningens hovedbæresystem (vist med grå skravur), mens gule kryss representerer trådbindere som ikke har noen beregningsmessig kapasitet. Gule kryss blir dermed kun montasjeforankring.

Lukk

Man må kontrollere at murverket har kapasitet til å spenne fritt mellom innfestingene. Det er aktuelt å bruke bruddlinjeteori eller forenklet beregning i henhold til informativt tillegg E i NS-EN 1996-1-1.

37Forankring til bakvegg med kjent stivhet

Der bakvegg har kjent stivhet og stivheten er i samme størrelsesorden som forblendingen, kan man benytte prinsippene for skallmur. Det vil si at lasten fordeles mellom forblendingen (ytre vange) og bakvegg (tilsvarende indre vange) etter stivhet, se Byggdetaljer 523.231. Det krever minst fire bindere per kvadratmeter som for skallmur.

38Ommurte hjørner

Ommurte hjørner er et typisk sted for sprekker. Årsaken til oppsprekking kan være at trådbindere er plassert for nært hjørnet, noe som hindrer at bevegelser i veggen kan tas opp av hjørnet. For å unngå fastlåsing av murverket ved hjørnet må trådbinderne plasseres minst 800 mm fra innsiden av ommurt hjørne, se fig. 38.

Man bør bruke fugearmering for omtrent hver halve høydemeter.

×

Fig. 38

Eksempel på ommurt hjørne. Horisontalsnitt

For ommurte hjørner må avstanden til første trådbinder være minst 800 mm.

Der man har utfordringer med å overholde minimumsavstanden mellom hjørne og binder, kan man kompensere ved å gjøre veggfeltet mindre.

Lukk

4Prosjektering og utførelse av bevegelsesfuger, glidesjikt og forankring

41Prosjektering

Plassering av bevegelsfuger bør gjøres i samarbeid med arkitekt. Den prosjekterende bør utarbeide en beskrivelse med tegninger som angir:

• plassering av bevegelsesfuger i fasaden

• opplegg for murveggen og om den skal utføres med eller uten glidesjikt

• type trådbindere og forankringssystem

• antall trådbindere

• plassering av konstruktive trådbindere

• festepunkt for isolasjon

• montasjeforankring

Videre bør det utarbeides en detalj som viser:

• hvordan trådbinderen mures inn i murvangen

• fri binderlengde

• forankringsdybde i bakvegg

Det anbefales å vise en prinsippdetalj for utførelse av bevegelsesfugen som viser fugebredde, bunnfylling og fugeform. Man bør beskrive krav til utførelse som rengjøring, priming, teiping og bestrøing.

Estetisk er det ønskelig at fugebredden til bevegelsesfugene er lik øvrige fuger. For teglvegger bør fugebredden være fra 1 mm per meter vegg. For vegger av andre murprodukter økes fugebredden tilpasset temperatur- og fuktbevegelsene.

Bevegelsesfuger kan utføres i forband, men en slik utførelse er mer krevende både teknisk og estetisk.

42Kontroll av bevegelsesfuger

Det er avgjørende at det ikke er mørtelrester i fugen. Selv små mengder mørtel kan skade veggen. Man bør kontrollere at bevegelsesfugene er frie for mørtel før fugene fylles med bunnfyllingslist og elastisk fugemasse.

43Prøvefelt

Det anbefales å mure et prøvefelt som inkluderer bevegelsesfuger. Prøvefeltene bygges med samme materialer og utførelse som er planlagt for prosjektet. Prøvefelt bør vurderes visuelt i både våt og tørr tilstand.

44Montering og innmuring av trådbindere

441Montering

Trådbinderen mures inn i horisontale mørtelfuger. Trådbinderen monteres slik at den får noe avstand til steinen under. Deretter legges mørtel før man legger på neste stein. Binderen skal omsluttes av fersk mørtel på alle sider. For skallmur, der bindere mures fast i indre vange, legger man mørtel først, før binderen dyttes ned i mørtelen og neste stein legges. Den enden av trådbinderen som mures inn, skal være bøyd i 90 graders vinkel. For at uttrekkskapasiteter fra tabell 34 skal være gjeldende, må tverrarmen (den bøyde enden) ha en lengde på minst 50 mm og en innmuringsdybde på minst 40 mm, se fig. 441. Hvis dette ikke er oppfylt, må kapasitet oppgis av leverandør eller det må gjennomføres tester. Vanligvis tilstrebes en sentrisk plassering av tverrarmen på teglvangen, slik at den plasseres ca. 50 mm inn på steinen for tegl i normalformat. I henhold til NS-EN 845-1 skal minste innmuringslengde være 30 mm. I tillegg må binderen omhylles med minst 20 mm mørtel for å hindre gjennomlokking (binderen trykkes gjennom murveggen).

×

Fig. 441

Minste forankringslengde ved innmuring av trådbinder i horisontalfuger

Lukk

442Bindere montert med fall

Bindere monteres med fall mot yttervange slik at binderne ikke leder vann fra ytre vange innover i veggen. Fallet bør være omtrent 1 : 15, men ikke mer enn 1 : 8. For mye fall vil redusere binderens lastkapasitet. For å redusere faren for at vann renner innover i veggen via binderne anbefales det å bruke isolasjonsholdere med dryppnese. Binderen skal stå i rett vinkel ut mot ytrevange i horisontalplanet. Binderen skal ikke bøyes andre steder enn for tverrarmen.

443Rette bindere

Det anbefales å montere bindere fortløpende samtidig med muringen og på en slik måte at binderne ikke påføres formfeil ved bøying. Hvis flere av binderne er bøyd, kan det medføre vesentlig redusert kapasitet.

45Montering av skrubinder

451Innskruingsdybde

Den gjengede delen av binderen skal skrus helt inn i det trevirket binderen forankres i. Hvis binderen ikke skrus direkte i trevirket, men for eksempel gjennom lekter og plater, blir det vanskelig å visuelt kontrollere at binderen er tilstrekkelig innskrudd, se fig. 451 b. I slike tilfeller anbefales det å bruke et monteringsverktøy som er tilpasset det aktuelle prosjektet, se fig. 451 a.

×

Fig. 451 a

Prinsippskisse av monteringsverktøy

Monteringsverktøy brukes for å sikre at binderen får nødvendig forankringslengde i trevirket.

Den lange enden er tilpasset slik at binderen skrus 50 mm inn i trevirket. Hvis binderen skrus gjennom lekter, må monteringsverktøyet kappes tilsvarende for å sørge for at binderen blir tilstrekkelig innskrudd i trevirket.

Lukk

×

Fig. 451 b

Eksempel på montering av skrubinder hvor man ikke har tatt hensyn til tykkelsen på vindsperreplata. Horisontalsnitt

Resultatet er at binderen ikke oppnår tilstrekkelig forankring i trevirket.

Lukk

452Binderens tverrarm (bøyd ende)

Binderens tverrarm (lengden av den bøyde enden) skal være minst 50 mm, og man bør tilstrebe å plassere den sentrisk i murvangen, se pkt. 441. Den korte enden av monteringsverktøyet benyttes til bøying av binderen slik at tverrarmen blir 50 mm, men verktøyet sikrer ikke at binderen plasseres midt i vangen med mindre binderen har akkurat riktig lengde. En praktisk løsning er å kutte den lange enden av monteringsverktøyet slik at man tilfredsstiller både kravet til lengde og plassering i vange. Figur 452 viser eksempler på hva som skjer ved feil bruk av innskruingsverktøy.

×

Fig. 452

Eksempel på feilmontert skrubinder. Horisontalsnitt

Binderens tverrarm er ikke sentrert i murvangen.

Lukk

453Kantavstand og bredde på trevirket

På grunn av krav til kantavstand, se pkt. 34, anbefales det å skru binderen inn i trevirke med en bredde på minst 48 mm. Binderen skal monteres i senter av trevirket den skal forankres i.

46Montering av slagbinder

461Boring av hull for slagbinder

Slagbinder monteres ved å bore et hull som slagbinderen slås inn i og dermed låses fast. Det anbefales å bruke spesialbor med dybdestopp, se fig. 461. Riktig diameter på bor og riktig dybde på hullet er avgjørende for at binderen får riktig kapasitet. For eksempel vil uttrekkskapasiteten til en slagbinder reduseres med 50 % dersom hullet bores til 70 % av foreskrevet dybde. Slagbinderen kan miste hele sin kapasitet dersom man borer for dypt eller med for stor diameter.

×

Fig. 461

Prinsippskisse av montering av slagbinder ved bruk av spesialbor med dybdestopp

Boret må være langt nok til å bore i korrekt vinkel uten å komme i konflikt med yttervangen.

Lukk

462Kantavstand

For en 4 mm slagbinder antas det full kapasitet med en kantavstand på minst 40 mm. For liten kantavstand reduserer kapasiteten. Kantavstand bør vies særlig oppmerksomhet ved montering i søyler eller dekkeforkanter, og da spesielt i hulldekker.

47Sjekkliste forankring

5Belastninger og kapasiteter

51Horisontallast

511Vindlast

Vindtrykk eller vindsug virker normalt på veggplanet og er vanligvis de lastene som blir dimensjonerende for forankringssystemets trykk- og strekkapasitet. Vindlast beregnes i henhold til NS-EN 1991-1-4.

512Jordskjelv

Byggverk dimensjoneres for seismiske laster i henhold til NS-EN 1998-1. [751] er en doktoravhandling fra NTNU om seismisk dimensjonering av trådbindere.

52Bevegelser

Variasjoner i temperatur og fuktighet gir bevegelser i murverket. Tabell 52 angir størrelsen på bevegelsene for ulike typer murprodukter og viser at temperaturvariasjon betyr mest for størrelsen på bevegelsene. Verdiene i tabellen er i henhold til NS-EN 1996-1-1.

Tegl har både en reversibel fuktutvidelse, $\mathsfit{\varepsilon_\mathsf{h}}$, i størrelsesorden 0,05 mm/m og en langtids irreversibel fuktutvidelse, $\mathsfit{\varepsilon_\mathsf{hu}}$, i størrelsesorden 0,5 mm/m. Reversibel fuktutvidelse, $\mathsfit{\varepsilon_\mathsf{h}}$, av tegl brukes sammen med temperaturbevegelser ved prosjektering av forankringssystemer.

For andre murprodukter enn tegl må det vurderes i hvor stor grad man skal ta hensyn til langtids fuktutvidelse/svinnkoeffisient, fordi engangs langtidseffekter har mindre påvirkning på forankringssystemet enn årlig pulserende bevegelser.

Årlig pulserende bevegelse, $\mathsfit{b}$ (mm/m), i murverket som følge av fukt- og temperaturutvidelse beregnes som:

$\mathsfit{b = \varepsilon_\mathsf{h} + \alpha_\mathsf{t} \cdot \Delta_\mathsf{t}}\qquad \textsf{(mm/m)}$

hvor:

• $\mathsfit{\varepsilon_\mathsf{h}}$ er reversibel fuktutvidelse (mm/m)

• $\mathsfit{\alpha_\mathsf{t}}$ er varmeutvidelseskoeffisient (m/mK), se tabell 52

• $\mathsfit{\Delta_\mathsf{t}}$ er den største temperaturdifferansen som veggen utsettes for i forhold til temperaturen på byggetidspunktet (K)

For klimadata for ulike steder, se Byggdetaljer 451.021. Det anbefales å bruke tredøgnsmiddel, $\mathsfit{\Phi_{3d}}$, som laveste temperatur. For høyeste temperatur må man gjøre en vurdering som tar høyde for soleksponering og veggfarge. Ved bygging i områder med spesielt lave vintertemperaturer eller andre spesielle forhold, anbefales det å beregne en prosjektspesifikk verdi for temperaturbevegelser. For murprodukter som ikke er tegl, må man benytte verdiene fra leverandøren for det aktuelle murproduktet. Skjønn og erfaringstall kan brukes.

SINTEF anbefaler å bruke en bevegelse på ±0,25 mm/m for tegl, som i tabellene i pkt. 23. Se pkt. 64 for beregningseksempel.

53Andre laster

531Brannlaster

Forblendinger med sammenhengende høyde på over 12 meter bør forankres til bygningens hovedbæresystem.

532Utmattingslaster

Utmattings- eller sprøbrudd kan være aktuelle bruddtyper. I henhold til NS-EN 846-5 og NS-EN 846-6 testes kapasiteten for bindere beregnet for sideveis forskyvning etter 50 sideveis forskyvninger med angitt maksimalt utslag før prøving. Kapasitet for stål i utmattelsesgrensetilstand kan også kontrolleres i henhold til NS-EN 1993-1-9.

54Tverrbelastning

541Sideveis forskyvning

Sideveis forskyvning (tverrbelastning) gir bøyemomenter i binderne og krefter som påvirker innspenningspunktet til binderne. Det kan føre til skader på murverket, innfesting av binderne og lokal overbelastning av tverrsnittet nær innfestingen. Bruksgrensetilstanden er dimensjonerende grensetilstand for tverrforskyvning, og det benyttes derfor en materialfaktor på 1,0 for tverrforskyvning. På grunn av momentbelastningen blir aksiallastkapasiteten redusert, men knekkingskapasiteten forblir uendret. Evne til å tåle sideveis forskyvning avhenger av lengden og stivheten til binderne.

542Fri binderlengde og beregningsmessig fri binderlengde

Fri binderlengde, slik den er definert i pkt. 18, er den geometriske avstanden mellom innspenningspunktene, for eksempel mellom innvendig side av yttervangen og bakveggen, sett bort fra vindsperreplater. Ved beregning av tverrbelastning benytter man en justert lengde, kalt beregningsmessig fri binderlengde, som tar hensyn til at bøying også skjer delvis inne i innspenningsmaterialet. For å ta hensyn til dette videre i beregningene, økes lengden med to ganger binderens diameter. Beregningsmessig fri binderlende, $\mathsfit{L_\mathsf{b}}$, er definert som:

$\mathsfit{L_\mathsf{b} = L + \mathsf{2} d}$

hvor:

• $\mathsfit{L}$ er fri binderlengde som definert i pkt. 18

• $\mathsfit{d}$ er binderens diameter

543Beregning av moment fra tverrforskyvning

Momentbelastning, $\mathsfit{M}_\mathsf{Ed}$, i binderen ved fast innspenning i begge ender beregnes etter følgende formel:

$\mathsfit{M_\mathsf{Ed} = \displaystyle\frac{\mathsf{6}\,\mathsfit{E}\,\mathsfit{I}}{\mathsfit{L}_\mathsf{b}^2} \,\mathsfit{\delta}_\mathsf{Ed}} \qquad \mathsfit{(Nmm)}$

hvor:

• $\mathsfit{E}$ er elastisitetsmodulen (N/mm²)

• $\mathsfit{I}$ er annet arealmoment (mm⁴)

• $\mathsfit{L_\mathsf{b}}$ er beregningsmessig fri binderlengde (mm)

• $\mathsfit{\delta}_\mathsf{Ed}$ er opptredende tverrforskyvning (mm)

En binder som er leddet i én ende, får halvparten av momentbelastningen til en binder som er fast innspent i begge endene.

Anbefalt maks pulserende tverrforskyvning for en binder gir så stor bøyning at binderen får plastiske, varige deformasjoner. Verdien framkommer ved å midle verdiene for et fullt utnyttet elastisk tverrsnitt og et fullt utnyttet (tenkt) tverrsnitt med plastisk momentkapasitet og elastisk tverrsnittsstivhet.

Maks pulserende tverrforskyvning for en trådbinder, $\mathsfit{\delta}_\mathsf{Rd}$, er:

$\mathsfit{ \delta_\mathsf{Rd} = \frac{ \displaystyle\frac{\mathsfit{M}_{\mathsf{Rd,pl}}\,\mathsfit{L}_\mathsf{b}^\mathsf{2}}{\mathsf{6}\,\mathsfit{E}\,\mathsfit{I}_{\mathsf{el}}} + \displaystyle\frac{\mathsfit{M}_{\mathsf{Rd,el}}\,\mathsfit{L}_\mathsf{b}^\mathsf{2}}{\mathsf{6}\,\mathsfit{E}\,\mathsfit{I}_{\mathsf{el}}} }{\displaystyle \mathsf{2}} } \qquad \mathsfit{(mm)}$

hvor:

• $\mathsfit{M_\mathsf{Rd,pl}}$ er plastisk momentkapasitet (Nmm)

• $\mathsfit{M_\mathsf{Rd,el}}$ er elastisk momentkapasitet (Nmm)

• $\mathsfit{E}$ er elastisitetsmodulen (N/mm²)

• $\mathsfit{L_b}$ er er binderens frie lengde (mm)

• $\mathsfit{I_{el}}$ er treghetsmomentet i elastisk tilstand (mm⁴)

 Utrykket kan skrives på følgende måte for innsetting av verdier:

$\mathsfit{ \delta_\mathsf{Rd} = \frac{ \displaystyle \mathsfit{f}\,(\mathsf{16} + \mathsf{3}\mathsf{\pi})\,(\mathsfit{L} + \mathsf{2}\mathsfit{d})^\mathsf{2} }{ \displaystyle \mathsf{18} \cdot \mathsfit{E} \cdot \mathsf{\pi} \cdot \mathsfit{d} } } \qquad \mathsfit{(mm)}$

hvor:

• $\mathsfit{f}$ er stålets flytegrense, minst 500 N/mm² (ofte 700 N/mm²)

• $\mathsfit{L}$ er fri binderlengde i henhold til pkt. 18 (mm)

• $\mathsfit{E}$ er stålets elastisitetsmodul, normalt 200 000 N/mm⁴

• $\mathsfit{d}$ er trådbinderens diameter, minst 4 mm

 Dermed kan største avstand fra nullpunkt for bevegelse, $\mathsfit{r}$, beregnes:

$\mathsfit{ r = \frac{ \displaystyle \mathsfit{\delta}_\mathsf{Rd} }{ \displaystyle \mathsfit{b} } }$

hvor:

• $\mathsfit{b}$ er bevegelsen for den aktuelle veggen (mm/m)

544Restkapasitet til aksiallast

I tabell 23 a–c benyttes materialfaktor $\mathsf{\gamma}_{\mathsf{S}}$ = 1,0. Det gir en restkapasitet ved plastisk betraktning av tverrsnittet som gjør at binderne selv ved maks sideveis forskyvning i henhold til tabell 23 a–c har kapasitet til aksialkrefter.

Momentkapasiteten for stål, $\mathsfit{M_\mathsf{NRd}}$, som er belastet med både bøyning og aksialkraft, er i henhold til NS-EN 1993-1-1:

$\mathsfit{ M_{\mathsf{NRd}} = \mathsfit{M_{\mathsf{Rd}}} \left[ \mathsf{1} - \left( \frac{\displaystyle \mathsfit{N}_{\mathsf{Ed}}}{\displaystyle \mathsfit{N}_{\mathsf{Rd}}} \right)^2 \right] } \qquad \mathsfit{(Nm)}$

hvor:

• $\mathsfit{M_\mathsf{Rd}}$ er momentkapasitet (Nm)

• $\mathsfit{N_\mathsf{Ed}}$ er aksialkraften (N)

• $\mathsfit{N_\mathsf{Rd}}$ er aksialkapasitet (N)

Det samme gjelder for aksialkapasiteten for stål som er belastet med både bøyning og aksialkraft:

$\mathsfit{ M_{\mathsf{Ed}} = M_{\mathsf{Rd}} \left[ \mathsf{1} - \left( \frac{\displaystyle \mathsfit{N}_{\mathsf{MRd}}}{\displaystyle \mathsfit{N}_{\mathsf{Rd}}} \right)^2 \right] } \qquad \mathsfit{(Nm)}$

hvor:

• $\mathsfit{M_{\mathsf{Ed}}}$ er påført moment (Nm)

• $\mathsfit{M_{\mathsf{Rd}}}$ er momentkapasitet (Nm)

• $\mathsfit{N_{\mathsf{MRd}}}$ er restaksialkapasitet ved momentbelastning (N)

• $\mathsfit{N_{\mathsf{Rd}}}$ er aksialkapasitet (N)

Restaksialkapasitet kan dermed uttrykkes som en funksjon av momentbelastningen:

$\mathsfit{ N_{\mathsf{MRd}} = \mathsfit{N}_{\mathsf{Rd}} \sqrt{\mathsf{1} - \left[ \left( \frac{\displaystyle \mathsfit{M}_{\mathsf{el}} + \mathsfit{M}_{\mathsf{pl}}}{\displaystyle \mathsf{2}} \right) \middle/ \mathsfit{M}_{\mathsf{pl}} \right]} = \mathsf{45\%} \cdot \mathsfit{N}_{\mathsf{Rd}} } \qquad \mathsfit{(N)}$

hvor:

• $\mathsfit{M_{\mathsf{el}}}$ er elastisk moment (N/m)

• $\mathsfit{M_{\mathsf{pl}}}$ er plastisk moment (N/m)

• $\mathsfit{N_{\mathsf{Rd}}}$ er aksialkapasitet (N)

Ved fullt utnyttet tverrforskyvning i henhold til anbefalingene i denne anvisningen, har den ytterste binderen utnyttet 55 % av tverrsnittets aksialkapasitet på tverrforskyvning.

55Aksialkapasitet

Trådbinderens evne til å overføre aksialkrefter er begrenset av knekklasten og tverrsnittskapasiteten. Trådbinderen kan betraktes som en stålsøyle belastet med aksialkraft. NS-EN 1993-1-1 angir beregningsregler for stålkonstruksjoner, inkludert imperfeksjonsfaktor, $\mathsfit{\alpha}$ = 0,49, og reduksjonsfaktor, $\chi$, for knekkingskontroll.

Reduksjonsfaktor, $\chi$, beregnes som:

 $\mathsfit{\chi = \dfrac{1}{\mathsfit{\varphi} + \sqrt{\mathsfit{\varphi}^{2} - \mathsfit{\lambda}^{2}}}}$

hvor:

 $\mathsfit{\varphi = \dfrac{1}{2} \left[ 1 + \mathsfit{\alpha} \left( \mathsfit{\lambda} - 0{,}2 \right) + \mathsfit{\lambda}^{2} \right] }$

$\mathsfit{\lambda}$ er slankheten:

 $\mathsfit{\lambda = \sqrt{\dfrac{\mathsfit{A} \cdot \mathsfit{f}_{\mathsf{yd}}}{\mathsfit{N}_{\mathsf{cr}}}} }$

$\mathsfit{N}_{\mathsf{cr}}$ er den kritiske knekklasten:

 $\mathsfit{N}_{\mathsf{cr}} = \dfrac{\mathsfit{\pi} \cdot \mathsfit{E} \cdot \mathsfit{I}}{\mathsfit{L}_{\mathsf{k}}^{\mathsf{2}}}$

hvor:

• $\mathsfit{E}$ er elastisitetsmodulen (N/mm²)

• $\mathsfit{I}$ er treghetsmomentet (mm⁴)

• $\mathsfit{L}_{\mathsf{k}}$ er lik 0,5 × L ved fast innspenning, 0,7 × L ved leddet ende og 2 × L ved fri ende (mm)

• $\mathsfit{L}$ er fri binderlengde som beskrevet i pkt. 18

Karakteristisk kapasitet er gitt ved formelen:

$\mathsfit{N}_{\mathsf{Rk}} = \mathsfit{\chi} \cdot \mathsfit{A} \cdot \mathsfit{f}_{\mathsf{yk}} \qquad \mathsfit{(N)}$

hvor:

• $\mathsfit{\chi}$ er reduksjonsfaktor

• $\mathsfit{A}$ er tverrsnittsarealet av binderen (mm²)

• $\mathsfit{f}_{\mathsf{yk}}$ er stålets karakteristiske flytegrense (N/mm²)

56Uttrekk av skrubinder fra trevirke

Karakteristisk uttrekkskapasitet finner man i leverandørens dokumentasjon, ved prøving i henhold til NS-EN 1382 eller ved beregning i henhold til NS-EN 1995-1-1. NS-EN 1995-1-1 angir at minste avstand til kanten skal være fire ganger skruediameteren, og tykkelsen på trevirket skal være 12 ganger skruediameter. Trevirket må derfor være minst 48 mm tykt.

Dimensjonerende uttrekkskapasitet, F_ax,d , beregnes med følgende formel:

$\mathsfit{F}_{\mathsf{ax,d}} = \mathsfit{f}_{\mathsf{ax,d}} \cdot \mathsfit{k} \qquad \mathsfit{(N)}$

hvor $\mathsfit{f}_{\mathsf{ax,d}}$ er karakteristisk uttrekkskapasitet.

 Korreksjonsfaktor for uttrekk fra trevirke, k, kan beregnes ut fra følgende formel:

$\mathsfit{k} = \dfrac{\mathsfit{k}_{\mathsf{mod}}}{\mathsfit{\gamma}_{\mathsf{m}}}$

hvor:

• $\mathsfit{k}_{\mathsf{mod}}$ er reduksjonsfaktor som tar hensyn til lastvarighet og fuktighet i trevirket

• $\mathsfit{\gamma}_{\mathsf{m}}$ er materialfaktor

Eksempel:

Dimensjonerende uttrekkskapasitet skal beregnes for en trådbinder innskrudd i trevirke.

En leverandør oppgir karakteristisk uttrekkskapasitet i konstruksjonstrevirke til 3500 N. NS-EN 1995-1-1 gir, i tillegg til materialfaktor, en reduksjonsfaktor, k_mod, som tar hensyn til lastvarighet og fuktighet i trevirket.

Vind er en korttidslast, og trevirket ligger innenfor vindsperresjiktet og dermed i klimaklasse 1.

Fra NS-EN 1995-1-1 hentes reduksjonsfaktor $\mathsfit{k}_{\mathsf{mod}}$ = 0,9 og vi benytter materialfaktor $\mathsfit{\gamma}_{\mathsf{m}}$ = 2,2. Korreksjonsfaktor for trevirket blir:

$\mathsfit{k} = \dfrac{\mathsfit{k}_{\mathsf{mod}}}{\mathsfit{\gamma}_{\mathsf{m}}} = \dfrac{\mathsf{0,9}}{\mathsf{2,2}} = \mathsf{0,41}$

Dimensjonerende uttrekkskapasitet blir:

$\mathsfit{F}_{\mathsf{ax,d}} = \mathsfit{f}_{\mathsf{ax,d}} \cdot \mathsfit{k} = \mathsf{3\;500} \mathsf{\;N} \cdot \mathsf{0,41} = \mathsf{1\;435} \mathsf{\;N}$

57Uttrekk av slagbindere fra betong og lettbetong

Uttrekk av slagbindere fra betong har vanligvis god kapasitet, ofte nær flytkapasiteten til selve binderen. Slagbindere er særlig sensitive for riktig montering for å oppnå full kapasitet, se pkt. 46. Byggdetaljer 573.144 beskriver ankerfester i betong, for bestemmelse av dimensjonerende kapasitet. Ved korrekt montering kan uttrekkskapasitet antas å være større enn det som gjelder for uttrekk fra murvange, som gitt i pkt. 34.

6Eksempel

61Beskrivelse av eksempel

En sørvendt armert teglfasade med glidesjikt skal deles opp i veggfelter med bevegelsesfuger. Bygningen ligger i fjellbygda Oppdal. Den er 15 meter høy og har ikke behov for horisontale bevegelsesfuger.

For å bestemme temperatur- og fuktbevegelsen i veggen antas det at veggen er oppført ved 11 °C, med en makstemperatur på 44 °C og en minimumstemperatur på −22 °C.

I eksempelet vurderes:

• bevegelser som murverket utsettes for

• plassering av bevegelsesfuger

• valg av forankringssystem

• beregning av vindlast

• kontroll av forankringssystem i forhold til opptredende vindlast

62Bevegelser

Teglveggen utsettes for temperaturdifferanse på ±33 °C. Se pkt. 61. Bevegelsen, b, som veggen utsettes for, kan dermed beregnes:

$\mathsfit{b} = \mathsfit{\varepsilon}_{\mathsf{h}} + \mathsfit{\alpha}_{\mathsf{t}} \cdot \mathsfit{\Delta}_{\mathsf{t}} = \mathsf{0,05} + \dfrac{\mathsf{6}}{\mathsf{1\;000}} \cdot \mathsf{33} = \mathsf{0,25} \qquad \mathsfit{(mm/m)}$

hvor:

• $\mathsfit{\varepsilon}_{\mathsf{h}}$ er fuktutvidelse-/svinnkoeffisient, se tabell 52

• $\mathsfit{\alpha}_{\mathsf{t}}$ er varmeutvidelseskoeffisient, se tabell 52

• $\mathsfit{\Delta}_{\mathsf{t}}$ er maks temperaturdifferanse veggen utsettes for i forhold til temperaturen på byggetidspunktet

Verdien b = 0,25 mm/m er den samme som i pkt. 23.

63Plassering av bevegelsesfuger

Tabell 241 angir at maks horisontalavstand for veggfeltet kan være 18 meter. Derfor må veggen deles opp i felter som er maks 18 meter lange.

64Valg av forankringssystem

Bevegelsesfugene plasseres med en avstand på 18 meter som beskrevet i pkt. 62. Det gir en avstand på 17,5 meter mellom nullpunkt for bevegelse og ytterste binder, se pkt. 22. Når avstanden er kjent, kan man vurdere de ulike forankringssystemene i pkt. 23. Nedenfor er eksempler på forankringssystemer som kan oppfylle kravet til avstand til ytterste binder.

Fast binder (hentet fra tabell 23 a):

• Fri binderlengde: 100 mm

• 4 mm trådbinder med stålkvalitet, f_yk = 700 N/mm²

Leddet binder (se tabell 23 b):

• Fri binderlengde: 75 mm

• 5 mm trådbinder med stålkvalitet, f_yk = 700 N/mm²

Forskyvelig binder (se tabell 23 c):

• Fri binderlengde: 50 mm

• 5 mm trådbinder med stålkvalitet, f_yk = 700 N/mm² kan brukes.

• 4 mm trådbinder med stålkvalitet, f_yk = 500 N/mm² gir 7,6 m fra nullpunkt horisontalt, og bredden på veggfeltet må i så fall begrenses fra 18 til 15,2 m.

65Vindlast

651Vindkasthastighetstrykk

Etter å ha valgt forankringssystem må man kontrollere om veggfeltet tåler de vindlastene det vil utsettes for.

Dette eksempelet bygger videre på et eksempel fra Byggdetaljer 471.044, hvor man bestemmer vindlasten for en bygning på Oppdal. Grunnverdien for hastighetstrykket, $\mathsfit{q}_{\mathsf{p0}(\mathsf{z})}$, er 0,84 kN/m², og man kan beregne vindkasthastighetstrykk, $\mathsfit{q}_{\mathsf{p}}$, etter følgende formel:

$\mathsfit{q}_{\mathsf{p}} = \mathsfit{q}_{\mathsf{p0}(\mathsf{z})} \cdot \mathsfit{k}_{1} \cdot \mathsfit{k}_{2} \cdot \mathsfit{k}_{\mathsf{R}} = \mathsf{0,84} \cdot \mathsf{1,2} \cdot \mathsf{1,45} \cdot \mathsf{1,07} = \mathsf{1,56} \qquad \mathsfit{(kN/m^{2})}$

hvor:

• k₁ er en faktor som tar hensyn til vindakselerasjonen over åser og skråninger

• k₂ er en faktor som tar hensyn til vindkastøkning nær fjelltopper eller særlig bratt terreng

• k_R er ruhetsfaktor som korrigerer vindlast med hensyn til bygningens avstand til åpent hav, store vidder og annet åpent terreng rundt byggestedet

652Dimensjonerende vindlast

For å finne dimensjonerende vindlaster må man bruke anbefalte verdier for utvendig formfaktor for vertikale vegger i rektangulære bygninger, som angitt i NS-EN 1991-1-4. Der henter man utvendig formfaktor, $\mathsfit{C}_{\mathsf{pe,10}}$, for utvendige flater større enn 10 m². Vanligvis benyttes verdiene fra sonene med størst trykk og sug for hele fasaden, da dette er til sikker side. Fra NS-EN 1991-1-4 hentes:

• utvendig formfaktor for sug, $\mathsfit{C}_{\mathsf{pe,10}}$ = −1,2

• utvendig formfaktor for trykk, $\mathsfit{C}_{\mathsf{pe,10}}$ = 0,8

Lastfaktoren for dominerende, variable, ugunstig last er i henhold til nasjonalt tillegg til NS-EN 1990:

• $\mathsfit{\gamma}_{\mathsf{Q,1}} = \mathsf{1,5}$

Dimensjonerende vindlast (trykk), $\mathsfit{E}_{\mathsf{dt}}$:

$\mathsfit{E}_{\mathsf{dt}} = \mathsfit{q}_{\mathsf{p}} \cdot \mathsfit{C}_{\mathsf{pe,10}} \cdot \mathsfit{\gamma}_{\mathsf{Q,1}} = \mathsf{1,56} \cdot \mathsf{0,8} \cdot \mathsf{1,5} = \mathsf{1,9} \qquad \mathsfit{(kN/m^{2})}$

Dimensjonerende vindlast (sug), $\mathsfit{E}_{\mathsf{ds}}$:

$\mathsfit{E}_{\mathsf{ds}} = \mathsfit{q}_{\mathsf{p}} \cdot \mathsfit{C}_{\mathsf{pe,10}} \cdot \mathsfit{\gamma}_{\mathsf{Q,1}} = \mathsf{1,56} \cdot \mathsf{(-1,2)} \cdot \mathsf{1,5} = \mathsf{-2,8} \qquad \mathsfit{(kN/m^{2})}$

hvor:

• $\mathsfit{q}_{\mathsf{p}}$ er vindkasthastighetstrykk på byggestedet (Oppdal)

• $\mathsfit{C}_{\mathsf{pe,10}}$ er utvendig formfaktor med betraktet belastet areal på 10 m²

• $\mathsfit{\gamma}_{\mathsf{Q,1}}$ er lastfaktor for dominerende variabel ugunstig last 

653Nødvendig antall trådbindere, vindtrykk

Når dimensjonerende vindlast er beregnet, kan tabellene i pkt. 33 brukes til å beregne nødvendige antall trådbindere for å motstå vindtrykk. Tabell 653 viser beregnet nødvendig antall bindere for de beskrevne konstruksjonene.

654Nødvendig antall trådbindere, vindsug

Det må også gjøres en beregning av nødvendig antall trådbindere som trengs for å motstå vindsug. I henhold til tabell 34 er uttrekkskapasiteten fra murvangen 680 N. Med et vindsug på 2,8 kN/m² er det nødvendige antallet trådbindere 4,1 stk./m². I tillegg må man kontrollere at uttrekkskapasiteten i bakveggen er minst like stor som i murvangen, se pkt. 34.

7Referanser

71Utarbeidelse

Denne anvisningen er utarbeidet av Fredrik Slapø i samarbeid med Tore Kvande (NTNU). Fagredaktør har vært Sondre Aasbø. Faglig redigering ble avsluttet i oktober 2025.

72Byggforskserien

Byggdetaljer:

451.021   Klimadata for termisk dimensjonering og frostsikring

471.044   Vindlaster på bygninger. Forenklet beregning av vindkasthastighetstrykk

523.231   Skallmurvegger

542.301   Murt forblending

570.001   Krav til produktdokumentasjon for omsetning og bruk av byggevarer

573.144   Ankerfester i betong

73Lover og forskrifter

Byggteknisk forskrift (TEK17) med veiledning

Forskrift om dokumentasjon av byggevarer (DOK)

74Standarder

NS-EN 845-1:2013 + A1:2016
Krav til tilbehør for murverk – Del 1: Veggbindere, strekkbånd, opplegg og konsoller

NS-EN 846-5:2012
Prøvingsmetoder for tilbehør til murverk – Del 5: Bestemmelse av veggbinderes strekk- og trykklastkapasitet og lastforskyvningsegenskaper (steinparprøving)

NS-EN 846-6:2012
Prøvingsmetoder for tilbehør til murverk – Del 6: Bestemmelse av veggbinderes strekk- og trykklastkapasitet og lastforskyvningsegenskaper (ensidig prøving)

NS-EN 998-2:2016
Krav til mørtel for murverk – Del 2: Murmørtel

NS-EN 1382:2016
Trekonstruksjoner – Prøvingsmetoder – Treforbindelsesmidlers uttrekkskapasitet

NS-EN 1990:2002 + A1:2005 + AC:2010 + NA:2016
Eurokode: Grunnlag for prosjektering av konstruksjoner

NS-EN 1991-1-4:2005 + NA:2009
Eurokode 1: Laster på konstruksjoner – Del 1–4: Allmenne laster – Vindlaster

NS-EN 1993-1-1:2005 + A1:2014 + NA:2015
Eurokode 3: Prosjektering av stålkonstruksjoner – Del 1–1: Allmenne regler og regler for bygninger

NS-EN 1993-1-9:2005 + NA:2010
Eurokode 3: Prosjektering av stålkonstruksjoner – Del 1–9: Utmattingspåkjente konstruksjoner

NS-EN 1995-1-1:2004 + A2:2014 + NA:2024
Eurokode 5: Prosjektering av trekonstruksjoner – Del 1–1: Allmenne regler og regler for bygninger

NS-EN 1996-1-1:2005 + A1:2012 + NA:2025
Eurokode 6: Prosjektering av murkonstruksjoner – Del 1–1: Allmenne regler for armerte og uarmerte murkonstruksjoner

NS-EN 1996-2:2006 + NA:2010
Eurokode 6: Prosjektering av murkonstruksjoner – Del 2: Valg av materialer og utførelse av murverk

NS-EN 1998-1:2004 + A1:2013 + NA:2021
Eurokode 8 – Prosjektering av konstruksjoner for seismisk påvirkning – Del 1: Allmenne regler, seismiske laster og regler for bygninger

75Litteraturhenvisninger

751A.M.Y. Hamed. Structural capacity of anchorage ties in masonry veneer walls subjected to earthquake: The implications of Eurocode 8 and Eurocode 6 on a typical Norwegian veneer wall. Ph.D.-avhandling, NTNU, 2011

Oktober 2025 ISSN 2387-6328